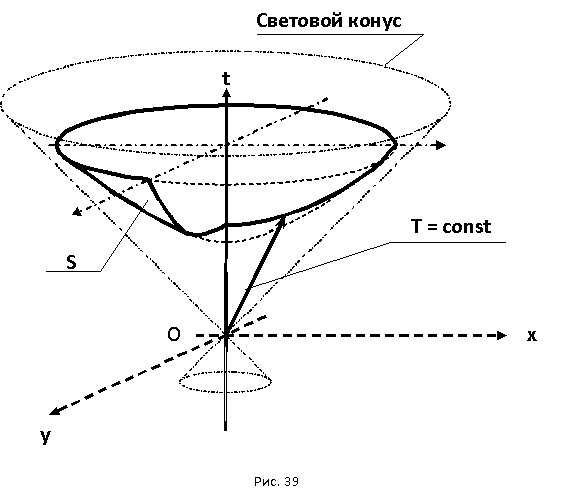
![Попарная независимостьСодержание а также Пример [ править ] § 4. Независимые события. Теорема умножения для независимых событий](http://www.dslib.net/i/d/4844/123977/450/4.png)
Лекции. Усиленный поток
Незав и симость в теории вероятностей, одно из важнейших понятий этой теории. В качестве примера можно привести определение Н. Событие В называется независимым от события А, если.
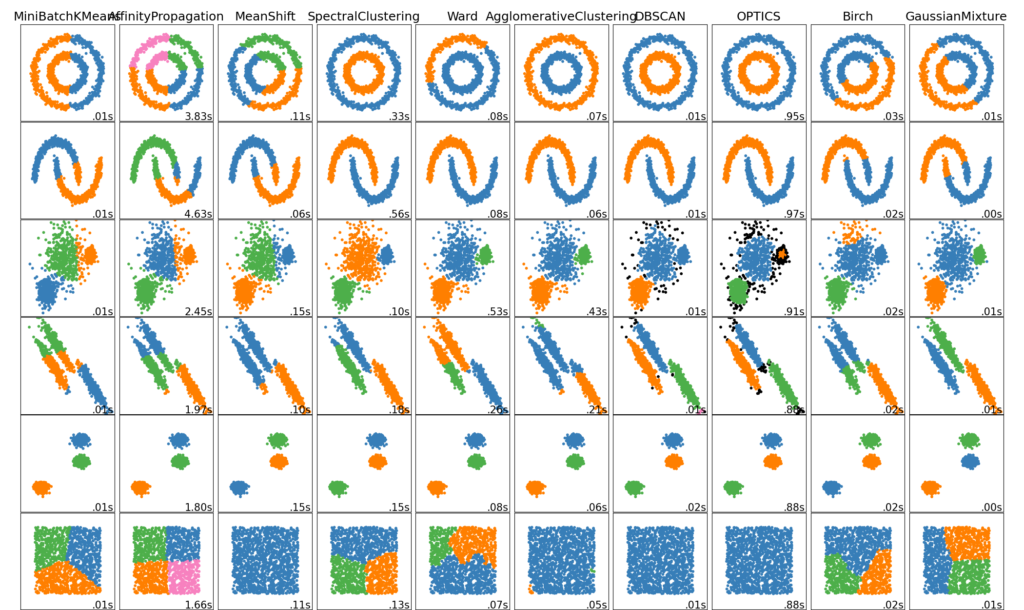

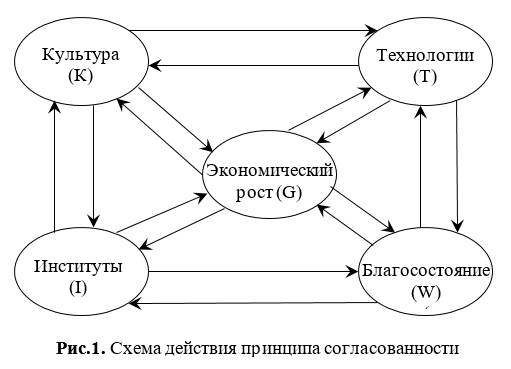

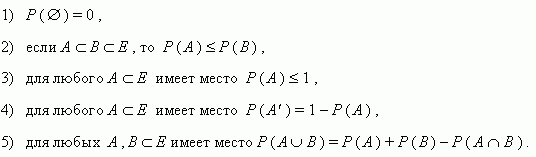



В частности, три события A, B и C будут попарно независимыми, если. События A 1 , A 2 , A 3 , … , A n называются взаимно независимыми или независимыми в совокупности , если для любого набора из этих n событий верно, что вероятность их одновременного появления равна произведению их вероятностей. В частности, три события A, B и C будут взаимно независимыми, если. Из этих двух определений следует, что если события взаимно независимые, то они обязательно попарно независимые.


.jpg)

Статистический смысл определения независимости проясняется при переходе от вероятностей событий к частотам: если производится большое число испытаний, то между частотой появления события A A A во всех испытаниях и частотой его появления в тех испытаниях, в которых происходит событие B B B , должно иметь место приближённое равенство. Независимость событий означает либо отсутствие связи между наступлением этих событий, либо несущественный характер этой связи. При определении независимости нескольких событий различают попарную и взаимную независимость. Однако в моделях теории вероятностей независимость обычно вводится как допущение. Понятие независимости переносится и на случайные величины. Аналогично определение независимости для нескольких случайных величин.